数据结构和算法（上）

一、本节介绍

1. 数据结构和算法

了解常用数据结构，掌握基本的算法思维，算法面试题的解题思路，同时复习常用数据结构和算法思维

2. 考察的重点

算法的时间复杂度和空间复杂度
三大算法思维：贪心，二分，动态规划
常见数据结构

3. 注意事项

算法，有难度，请耐心学习
一个问题的解决方案有很多，要找出最优解（重要）
不仅关注题目本身，更要关注知识点和解题思路

二、科普 - 算法复杂度

1. 什么是复杂度

程序执行时需要的计算量和内存空间（和代码是否简洁无关）
复杂度是 数量级（方便记忆、推广），不是具体的数字。用 O(...) 表示，内部是一个函数表达式
一般针对于一个具体的算法，而并非一个完整的系统

2. 时间复杂度

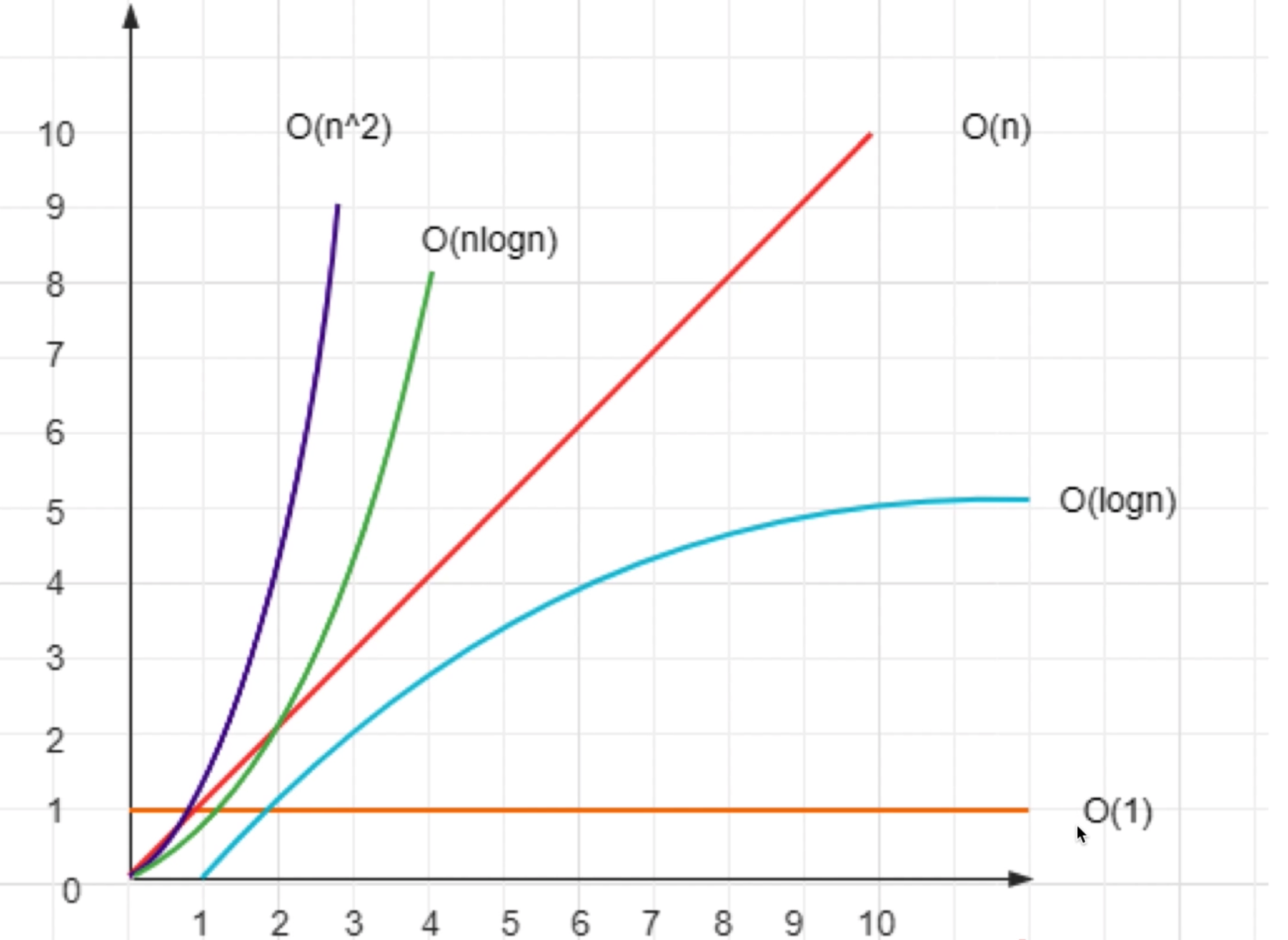
程序执行时需要的计算量（ CPU ）
1. O(1) - 一次就够（数量级）
2. O(n) - 和传输的数据量一样（数量级）
3. O(n^2) - 数据量的平方（数量级）
4. O(logn) - 数据量的对数（数量级）
5. O(nlogn) - 数据量 * 数据量的对数（数量级）

3. 空间复杂度

程序执行时需要的内存空间
1. O(1) - 有限的、可数的空间（数量级）
2. O(n) - 和传入的数据量相同的空间（数量级）

4. 必须掌握算法复杂度

如果没有复杂度的概念和敏感度，写程序是非常危险的
例如：代码功能测试正常，但是数量大了，程序就会崩溃
对于前端开发，尤其是时间复杂度
复杂度达到 O(n^2) 算法基本上就是不可用的

三、把一个数组旋转 k 步

1. 题目

输入一个数组 [1, 2, 3, 4, 5, 6, 7]
k = 3 , 即旋转 3 步
输出 [5, 6, 7, 1, 2, 3, 4]

2. 解题思路

思路一：把末尾的元素挨个 pop ，然后 unshift 到数组前面
思路二：把数组拆分，最后 concat 拼接到一起

3. 代码

typescript

/**
 * 旋转数组 k 步 - 方法一：使用 pop 和 unshift
 * @param arr
 * @param k
 * @return arr
 */
export function rotate1(arr: number[], k: number): number[] {
    const length = arr.length;
    if (length === 0 || !k) return arr
    const step = Math.abs(k % length)  // abs 绝对值
    // O(n^2)
    for (let i = 0; i < step; i++) {  // O(n)
        const n = arr.pop()
        n != null && (arr.unshift(n))  // O(n) 数组是个有序结构, unshift 操作非常慢!!!
    }
    return arr
}

// 正确答案
/**
 * 旋转数组 k 步 - 方法二：使用 concat
 * @param arr
 * @param k
 * @return arr
 */
export function rotate2(arr: number[], k: number): number[] {
    const length = arr.length;
    if (length === 0 || !k) return arr
    const step = Math.abs(k % length)  // abs 绝对值
    
    // O(1)
    const part1 = arr.slice(-step)
    const part2 = arr.slice(0, length - step)
    return part1.concat(part2)
}

4. 单元测试

typescript

/**
 * @description 数组旋转 k 部
 * @author lzz
 */
import {rotate1, rotate2} from './1. 数组旋转 k 步'

const arr = [1, 2, 3, 4, 5, 6, 7]

describe('数组旋转 k 部', () => {
    it('正常情况下', () => {
        const k = 3
        const res = rotate2(arr, k)
        expect(res).toEqual([5, 6, 7, 1, 2, 3, 4])  // 断言 返回值为对象或数组用 toEqual
    })
    it('数组为空', () => {
        const res = rotate2([], 3)
        expect(res).toEqual([])
    })
    it('k 是负值', () => {
        const k = -3
        const res = rotate2(arr, k)
        expect(res).toEqual([5, 6, 7, 1, 2, 3, 4])  // 断言
    })
    it('k 不是数字', () => {
        const k = 'abc'
        // @ts-ignore
        const res = rotate2(arr, k)
        expect(res).toEqual(arr)  // 断言
    })
    it('k 不是 0', () => {
        const k = 0
        const res = rotate2(arr, k)
        expect(res).toEqual(arr)  // 断言
    })
})

5. 性能测试

思路一：时间复杂度 O(n^2) ，空间复杂度 O(1)
思路二：时间复杂度 O(1) ，空间复杂度 O(n)

typescript

// 性能测试
const arr1 = []
const arr2 = []

for (let i = 0; i < 10 * 10000; i++) {
    arr1.push(i)
    arr2.push(i)
}

console.time('rotate1')
rotate1(arr1, 9 * 10000)  // 891.36 ms
console.timeEnd('rotate1')

console.time('rotate2')
rotate2(arr2, 9 * 10000)  // 0.45 ms
console.timeEnd('rotate2')

6. 划重点

注意算法复杂度（前端重时间，轻空间）
识破内置 API 的时间复杂度（如：unshift ）
单元测试，考虑参数非法情况，提升代码健壮性
不要过度优化，比复杂度更重要的是代码逻辑清晰、易读

四、判断字符串是否括号匹配

1. 题目

一个字符串 s 可能包括 {} () [] 三种括号
判断 s 是否是括号匹配的
如 (a{b}c) 匹配，而 {a(b 或 {a(b}c) 就不匹配

2. 前置知识

考察知识点 - 栈
1. 先进后出
2. 相关 API：push pop length
3. 相关知识点：队列，堆（后面有）

栈 - 代码演示

typescript

const stack = []
stack.push(100)  // 入栈（压栈）
stack.push(200)
stack.push(300)
const num = stack.pop()  // 出栈
console.log(stack.length)  // 栈长

1. 栈 vs 数组
2. 栈：逻辑结构，理论模型。不管如何实现，不受任何语言限制
3. 数组：物理结构。真实的功能实现，受限于编程语言

3. 解题思路

遇到左括号 { [ ( 就压栈
遇到 ) ] } 就匹配栈顶，匹配则出栈，不匹配直接返回 false
最后判断 length 是否为 0

4. 代码

typescript

/**
 * 括号匹配
 * @param str
 * @return boolean
 */
export function matchBracket(str: string): boolean {
    const length = str.length
    if (!length) return true;
    const stack = []
    const leftSymbol = '{(['
    const rightSymbol = '})]'
    for (let i = 0; i < length; i++) {
        const item = str[i]
        // 数据量固定，不计算 includes 的复杂度
        if (leftSymbol.includes(item)) {
            // 左括号, 压栈
            stack.push(item)
        } else if (rightSymbol.includes(item)) {
            // 右括号, 判断栈顶 (是否出栈)
            if (isMatch(stack[stack.length - 1], item)) {
                stack.pop()
            } else {
                return false
            }
        }
    }
    return stack.length === 0
}

/**
 * 判断左右括号是否匹配
 * @param left
 * @param right
 * @return boolean
 */
function isMatch(left: string, right: string): boolean {
    if (left) {
        if (left === '{' && right === '}') return true
        if (left === '(' && right === ')') return true
        return left === '[' && right === ']';
    } else {
        return false
    }
}
// function isMatch(left: string, right: string): boolean {
//     const map = ['{}', '()', '[]']
//     return map.includes(`${left}${right}`)
// }

5. 单元测试

typescript

/**
 * @description 括号匹配 test
 * @author lzz
 */
import {matchBracket} from './2. 判断字符串是否括号匹配'

describe('括号匹配', () => {
    it('正常情况', () => {
        const str = '{1(2)[3]}'
        const res = matchBracket(str)
        expect(res).toBe(true)  // 布尔类型要使用 toBe (精确匹配)
    })

    it('不匹配', () => {
        const str = '{1((2)[3]}'
        const res = matchBracket(str)
        expect(res).toBe(false)
    })

    it('顺序不一致', () => {
        const str = '{1(2[3]})'
        const res = matchBracket(str)
        expect(res).toBe(false)
    })

    it('空字符串', () => {
        const res = matchBracket('')
        expect(res).toBe(true)
    })
})

6. 性能测试

时间复杂度 O(n)
空间复杂度 O(n)

7. 划重点

栈
逻辑结构 vs 物理结构

五、两个栈实现一个队列

1. 题目

请用两个栈，实现一个队列
功能 add delete length

2. 前置知识

队列
1. 先进先出
2. API：add delete length

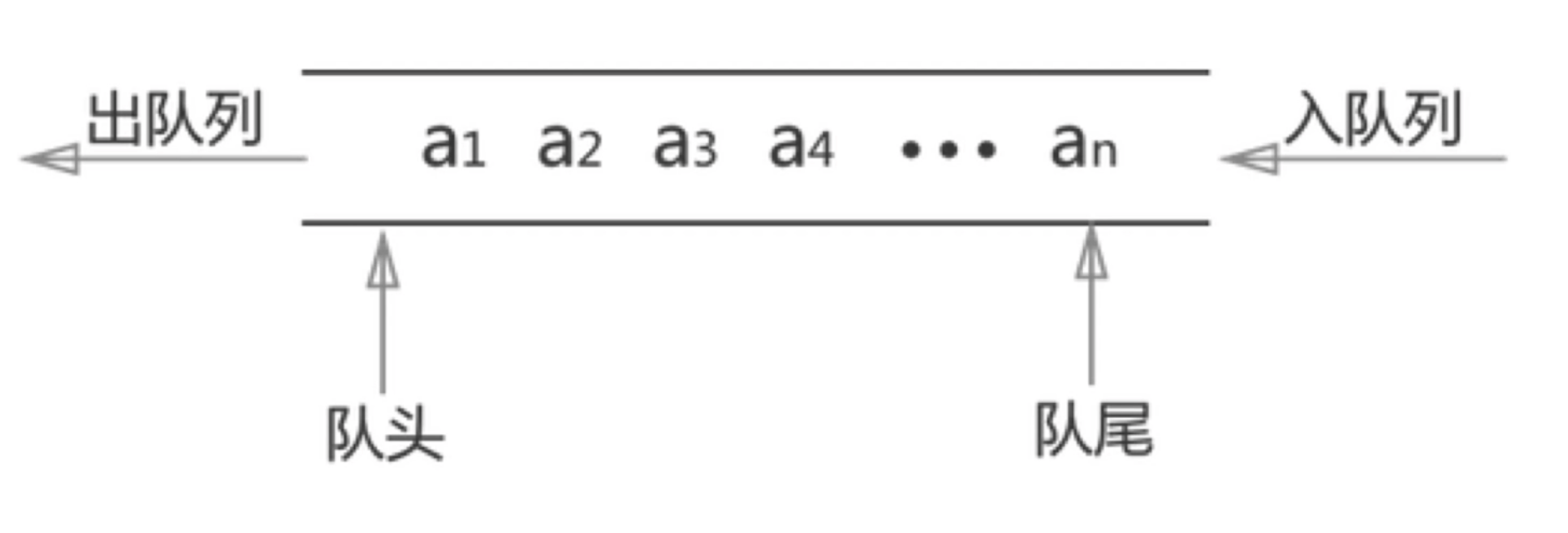
队列 - 代码演示

typescript

const queue = []
queue.push(100)  // 入队
queue.push(200)
queue.push(300)
const n = queue.shift()  // 出队

1. 队列是逻辑结构，抽象模型
2. 可以简单的用数组、链表（后面有）实现
3. 复杂的队列服务，需要单独的设计

3. 解题思路

4. 代码

typescript

/**
 * @description 两个栈实现一个队列
 * @author lzz
 */
export class MyQueue {
    private stack1: number[] = []
    private stack2: number[] = []

    /**
     * 入队
     * @param n number
     */
    add(n: number) {
        this.stack1.push(n)
    }

    /**
     * 出队
     */
    delete(): number | null {
        let res
        const stack1 = this.stack1
        const stack2 = this.stack2

        // 1. 将 stack1 所有元素移动到 stack2 中
        while (stack1.length) {
            const n = stack1.pop()
            if (n != null) stack2.push(n)
        }

        // 2. stack2 pop
        res = stack2.pop()

        // 3. 将 stack2 中所有元素 "还给" stack1
        while (stack2.length) {
            const n = stack2.pop()
            if (n != null) stack1.push(n)
        }

        return res || null
    }

    // 函数前加 get , 就可以使用属性形式调用 ( .length )
    get length(): number {
        return this.stack1.length
    }
}

5. 单元测试

typescript

/**
 * @description 两个栈实现一个队列
 * @author lzz
 */
import {MyQueue} from './3. 两个栈实现一个队列'

describe('两个栈实现一个队列', () => {
    it('add and length', () => {
        const q = new MyQueue();
        expect(q.length).toBe(0)
        q.add(100)
        q.add(200)
        q.add(300)
        expect(q.length).toBe(3)
    })

    it('delete', () => {
        const q = new MyQueue();
        expect(q.delete()).toBeNull()
        q.add(100)
        q.add(200)
        q.add(300)
        expect(q.delete()).toBe(100)
        expect(q.length).toBe(2)
        expect(q.delete()).toBe(200)
        expect(q.length).toBe(1)
    });
})

6. 性能分析

时间复杂度：add O(1) ; delete O(n)
空间复杂度：整体是 O(n)

7. 划重点

队列
逻辑结构 vs 物理结构
画图，帮忙梳理解题思路

六、定义一个 JS 函数，反转单向链表

1. 前置知识

链表是一种物理结构（非逻辑结构），**类似 **于数组
数组需要一段连续的内存空间，而链表是零散的
链表节点的数据结构 { data, next?, prev?(双链表才有) }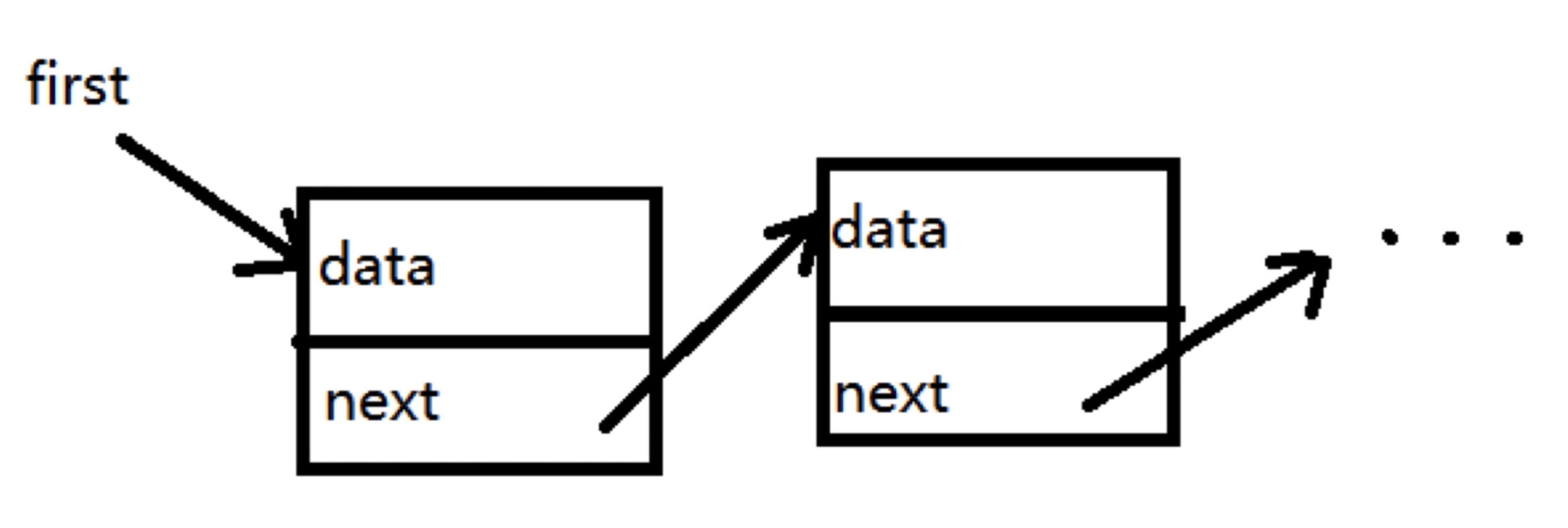

代码演示

typescript

// 双链表结构
const n1 = {
    data: '100',
    next: n2
}
const n2 = {
    data: '200',
    next: n3,
    prev: n1
}
const n3 = {
    data: '300',
    next: n4,
    prev: n2
}
const n4 = {
    data: '400',
    prev: n3
}

根据数组创建单向链表

typescript

/**
 * @description 反转单向链表
 * @author lzz
 */

interface ILinkListNode {
    data: number
    next?: ILinkListNode
}

/**
 * 根据数组创建单向链表
 * @param arr
 */
function createLinkList(arr: number[]): ILinkListNode {
    const length = arr.length
    if (!length) throw new Error("array is empty")
    let curNode: ILinkListNode = {
        data: arr[length - 1]
    }
    if (length === 1) {
        return curNode
    } else {
        for (let i = length - 2; i >= 0; i--) {
            curNode = {
                data: arr[i],
                next: curNode
            }
        }
    }
    return curNode
}

链表 vs 数组
1. 都是有序结构（对象就是无序结构）
2. 链表：查询慢 O(n)，新增、删除快 O(1)
3. 数组：查询快 O(1)，新增、删除慢 O(n)
4. 扩展应用：React Fiber 使用了链表（了解即可）

3. 解题思路

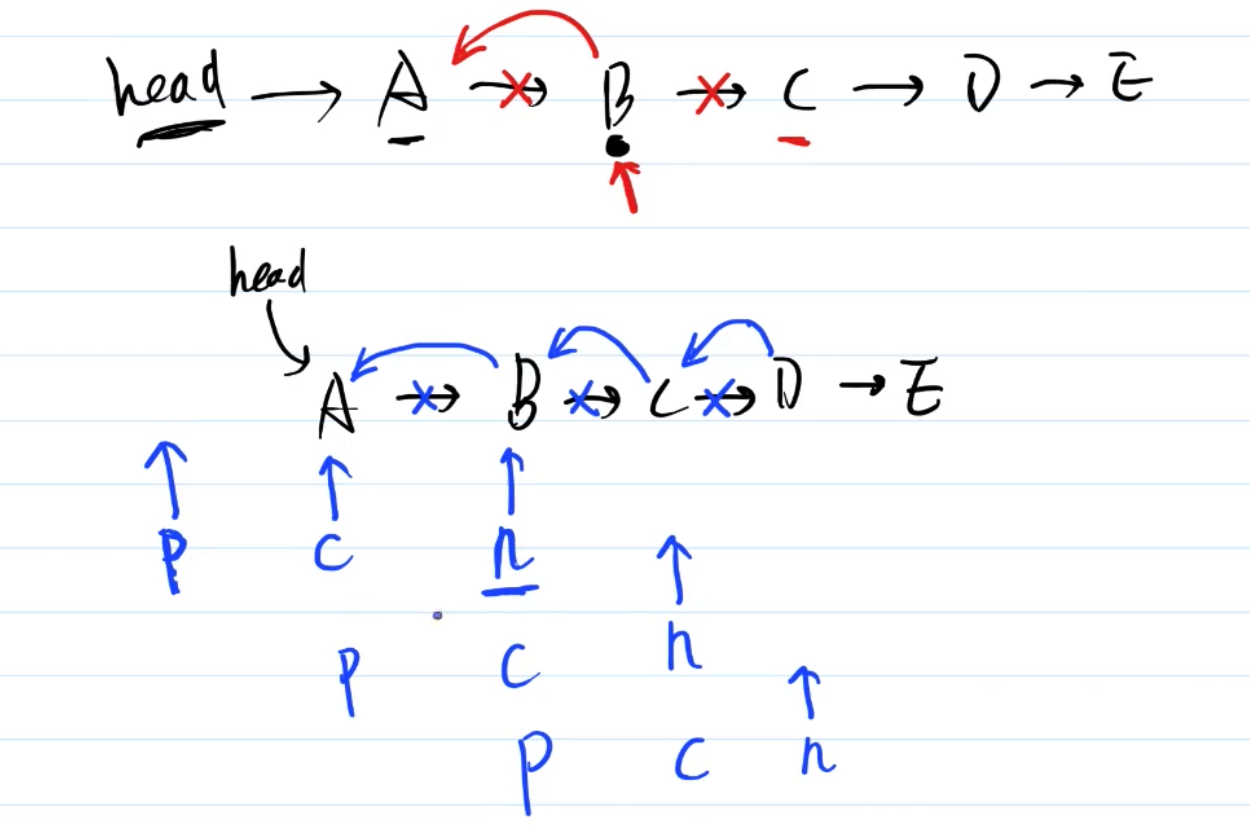
反转，即节点 next 指向前一个节点
但很容易造成 nextNode 的丢失
需要三个指针 prevNode curNode nextNode

4. 代码

typescript

/**
 * 反转单向链表, 并返回反转后的单向链表
 * @param listNode list head node
 */
export function reverseLinkList(listNode: ILinkListNode): ILinkListNode {
    // 定义三个指针(变量)
    let prevNode: ILinkListNode | undefined = undefined
    let curNode: ILinkListNode | undefined = undefined
    let nextNode: ILinkListNode | undefined = listNode

    // 以 nextNode 为主, 遍历链表
    while (nextNode) {
        // 第一个元素, 删掉 next, 防止循环引用
        if (curNode && !prevNode) {
            delete curNode.next
        }
        // 反转指针
        if (curNode && prevNode) {
            curNode.next = prevNode
        }
        // 整体向后移动指针
        prevNode = curNode
        curNode = nextNode
        nextNode = nextNode?.next
    }
    // 最后一个的补充: 当 nextNode 空时, 此时 curNode 尚未设置 next
    // ! 是指告诉程序, curNode 确定不为空
    curNode!.next = prevNode

    return curNode!
}

5. 单元测试

typescript

/**
 * @description 反转单向链表
 * @author lzz
 */
import {ILinkListNode, reverseLinkList, createLinkList} from "./4. 定义函数 反转单链表"

describe("反转单向链表", () => {
    it('单个元素 ', () => {
        const node: ILinkListNode = {data: 100}
        const node1 = reverseLinkList(node)
        expect(node1).toEqual({data: 100})
    });
    it('多个元素', () => {
        const node = createLinkList([100, 200, 300])
        const node1 = reverseLinkList(node)
        expect(node1).toEqual({
            data: 300,
            next: {
                data: 200,
                next: {
                    data: 100
                }
            }
        })
    });
})

6. 划重点

链表，链表 vs 数组
如何让 nextNode 不丢失
链表的代码逻辑比较繁琐，调试成本高

七、（连环问）链表和数组，那个实现队列更快

1. 分析

数组时连续存储，push 很快，shift 很慢
链表是非连续存储，add 和 delete 都很快（但查找很慢）
结论：链表实现队列会更快

2. 题目

用链表实现队列

3. 解题思路

单向链表，但是同时记录 head 和 tail
要从 tail 入队，从 head 出队，否则出队时 tail 不好定位
length 要实时记录，不可遍历链表时获取

4. 代码

typescript

/**
 * @description 用链表实现队列
 * @author lzz
 */
interface IListNode {
    data: number
    next: IListNode | null
}

export class MyQueue {
    private head: IListNode | null = null
    private tail: IListNode | null = null
    private len = 0

    /**
     * 入队, 在 tail 位置
     * @param n
     */
    add(n: number) {
        const newNode: IListNode = {
            data: n,
            next: null
        }

        // 处理 head
        if (this.head == null) this.head = newNode

        // 处理 tail
        const tailNode = this.tail
        if (tailNode) tailNode.next = newNode
        this.tail = newNode

        // 记录长度
        this.len += 1
    }

    /**
     * 出队, 在 head 位置
     */
    delete(): number | null {
        const headNode = this.head
        if (headNode == null || this.len === 0) return null

        // 取值
        const data = headNode.data

        // 处理 head
        this.head = headNode.next

        // 记录长度
        this.len -= 1
        return data
    }

    get length(): number {
        // length 要单独存储, 不能遍历链表 ( 否则时间复杂度太高 - O(n) )
        return this.len
    }
}

6. 单元测试

typescript

/**
 * @description 用链表实现队列
 * @author lzz
 */
import {MyQueue} from './5.用链表实现队列'

describe('用链表实现队列', () => {
    it('add and length', () => {
        const q = new MyQueue()
        expect(q.length).toBe(0)
        q.add(100)
        q.add(200)
        q.add(300)
        expect(q.length).toBe(3)
    })
    it('delete', () => {
        const q = new MyQueue()
        expect(q.delete()).toBeNull()
        q.add(100)
        q.add(200)
        q.add(300)
        expect(q.delete()).toBe(100)
        expect(q.delete()).toBe(200)
        expect(q.delete()).toBe(300)
        expect(q.delete()).toBeNull()
    })
})

7. 性能测试

typescript

// 性能测试
const q1 = new MyQueue()
console.time('queue with list')
for (let i = 0; i < 10 * 10000; i++) {
    q1.add(i)
}
for (let i = 0; i < 10 * 10000; i++) {
    q1.delete()
}
console.timeEnd('queue with list')  // 8.25ms

const q2 = []
console.time('queue with arr')
for (let i = 0; i < 10 * 10000; i++) {
    q2.push(i)
}
for (let i = 0; i < 10 * 10000; i++) {
    q2.shift()
}
console.timeEnd('queue with arr')  // 14.41s

空间复杂度都是 O(n)
add 时间复杂度：链表 O(1) ；数组 O(1)
delete 时间复杂度：链表 O(1)；数组 O(n)

8. 划重点

链表，链表 vs 数组
数据结构的选择，要比算法优化更重要
要有时间复杂度的敏感性，如 length 不能遍历查找

八、实现二分查找

1. 题目

用 JavaScript 实现二分查找
并说明时间复杂度

2. 解题思路

递归 - 代码逻辑更加清晰
非递归 - 性能更好
时间复杂度 O(logn) -- 非常快！

3. 代码

使用循环

typescript

/**
 * 二分查找 (循环)
 * @param arr arr
 * @param target target
 */
function binarySearch1(arr: number[], target: number): number {
    const len = arr.length
    if (len === 0) return -1
    let startIndex = 0  // 开始位置
    let endIndex = len - 1  // 结束位置
    while (startIndex <= endIndex) {
        const midIndex = Math.floor((startIndex + endIndex) / 2)
        const midValue = arr[midIndex]
        if (target < midValue) {
            // 目标值较小, 则继续从左侧查找
            endIndex = midIndex - 1
        } else if (target > midValue) {
            // 目标值较大, 则继续从右侧查找
            startIndex = midIndex + 1
        } else {
            // 相等, 返回
            return midIndex
        }
    }
    return -1
}

使用递归

typescript

/**
 * 二分查找 (递归)
 * @param arr
 * @param target
 * @param startIndex start index
 * @param endIndex end index
 */
function binarySearch2(arr: number[], target: number, startIndex?: number, endIndex?: number): number {
    const len = arr.length
    if (len === 0) return -1
    // 开始和结束的范围
    if (startIndex == null) startIndex = 0
    if (endIndex == null) endIndex = len - 1
    // 如果 startIndex 和 endIndex 相遇, 则结束
    if (startIndex > endIndex) return -1
    // 中间位置
    const midIndex = Math.floor((startIndex + endIndex) / 2)
    const midValue = arr[midIndex]
    if (target < midValue) {
        // 目标值较小, 则继续从左侧查找
        return binarySearch2(arr, target, startIndex, midIndex - 1)
    } else if (target > midValue) {
        // 目标值较大, 则继续从右侧查找
        return binarySearch2(arr, target, midIndex + 1, endIndex)
    } else {
        // 相等, 返回
        return midIndex
    }
}

4. 单元测试

typescript

/**
 * @description 二分法查找
 * @author lzz
 */

import {binarySearch1, binarySearch2} from './6. 二分法查找'

const arr = [10, 20, 30, 40, 50, 60]

describe('二分法查找', () => {
    it('正常情况', () => {
        expect(binarySearch1(arr, 30)).toBe(2)
    })

    it('arr 为空', () => {
        expect(binarySearch1([], 30)).toBe(-1)
    })

    it('target 找不到', () => {
        expect(binarySearch1(arr, 90)).toBe(-1)
    })
})

5. 性能测试

typescript

// 较真来说，循环和递归哪个更快（循环 - 不是数量级）
const arr = [10, 20, 30, 40, 50]

console.time('binarySearch1')
for (let i = 0; i < 100 * 10000; i++) {
    binarySearch1(arr, 40)
}
console.timeEnd('binarySearch1')  // 11.32ms

console.time('binarySearch2')
for (let i = 0; i < 100 * 10000; i++) {
    binarySearch2(arr, 40)
}
console.timeEnd('binarySearch2')  // 15.48ms

// 调用函数也有开销

6. 划重点

凡有序，必二分！！！
凡二分，时间复杂度必包含 O(logn) ！！！
递归 vs 非递归

九、找出数组中和为 n 的两个元素

1. 题目

有一个递增的数组 [1, 2, 4, 7, 11, 15] 和 n = 15
数组中有 两个数 和是 n ，即 4 + 11 === 15
写一个 js 函数，找出这两个数

2. 常规思路

嵌套循环，找到一个数，然后去遍历下一个数，求和，判断

时间复杂度是 O(n^2) ，不可用

typescript

/**
 * 嵌套循环查找两数之和
 * @param arr arr
 * @param n n
 */
function findNumbers1(arr: number[], n: number): number[] {
    const len = arr.length;
    const result: number[] = []
    if (len === 0) return arr
    // O(n^2)
    for (let i = 0; i < len - 1; i++) {
        let flag = false
        const n1 = arr[i]
        for (let j = i + 1; j < len; j++) {
            const n2 = arr[j]
            if (n1 + n2 === n) {
                result.push(n1)
                result.push(n2)
                flag = true
                break
            }
        }
        if (flag) break
    }
    return result
}

3. 解题思路

利用递增（有序）的特性
1. 首尾找两个数
2. 如果和大于 n ，则需要向前寻找
3. 如果和小于 n ，则需要向后寻找 - 二分法思想

双指针，时间复杂度降低到 O(n)
1. 定义 i 指向头，j 指向尾，求 arr[i] + arr[j]
2. 如果大于 n，则 j 需要向前移动
3. 如果小于 n，则 i 需要向后移动

4. 代码

typescript

/**
 * 双指针查找两数之和
 * @param arr
 * @param n
 */
export function findNumbers2(arr: number[], n: number): number[] {
    const res: number[] = []
    const len = arr.length
    if (!len) return []
    let i = 0  // 头指针
    let j = len - 1  // 尾指针
    while (i < j) {
        const n1 = arr[i]
        const n2 = arr[j]
        const sum = n1 + n2
        if (sum > n) {
            // sum 大于 n, 则 j 需要向前移动
            j--
        } else if (sum < n) {
            // sum 小于 n, 则 j 需要向后移动
            i++
        } else {
            // 相等
            res.push(n1)
            res.push(n2)
            break
        }
    }
    return res
}

5. 单元测试

typescript

/**
 * @description 找出数组中和为 n 的两个元素
 * @author lzz
 */
import {findNumbers1, findNumbers2} from './7. 找出数组中和为 n 的两个元素'

const arr = [1, 2, 4, 7, 11, 15]

describe("找出数组中和为 n 的两个元素", () => {
    it('正常情况下', () => {
        expect(findNumbers2(arr, 15)).toEqual([4, 11])
    })

    it('数组为空', () => {
        expect(findNumbers2([], 15)).toEqual([])
    })

    it('找不到情况下', () => {
        expect(findNumbers2(arr, 100)).toEqual([])
    })
})

6. 性能测试

typescript

const array: number[] = [1, 2, 4, 7, 11, 15]

console.time('findNumbers1')
for (let i = 0; i < 100 * 10000; i++) {
    findNumbers1(array, 15)
}
console.timeEnd('findNumbers1')  // 42.23ms

console.time('findNumbers2')
for (let i = 0; i < 100 * 10000; i++) {
    findNumbers2(array, 15)
}
console.timeEnd('findNumbers2')  // 28.82ms

7. 划重点

时间复杂度达到 O(n^2) ，是不可用的算法
凡有序，必二分！！！
优化嵌套循环，可以考虑 “双指针”

数据结构和算法（上） ​

一、本节介绍 ​

1. 数据结构和算法 ​

2. 考察的重点 ​

3. 注意事项 ​

二、科普 - 算法复杂度 ​

1. 什么是复杂度 ​

2. 时间复杂度 ​

3. 空间复杂度 ​

4. 必须掌握算法复杂度 ​

三、把一个数组旋转 k 步 ​

1. 题目 ​

2. 解题思路 ​

3. 代码 ​

4. 单元测试 ​

5. 性能测试 ​

6. 划重点 ​

四、判断字符串是否括号匹配 ​

1. 题目 ​

2. 前置知识 ​

3. 解题思路 ​

4. 代码 ​

5. 单元测试 ​

6. 性能测试 ​

7. 划重点 ​

五、两个栈实现一个队列 ​

1. 题目 ​

2. 前置知识 ​

3. 解题思路 ​

4. 代码 ​

5. 单元测试 ​

6. 性能分析 ​

7. 划重点 ​

六、定义一个 JS 函数，反转单向链表 ​

1. 前置知识 ​

3. 解题思路 ​

4. 代码 ​

5. 单元测试 ​

6. 划重点 ​

七、（连环问）链表和数组，那个实现队列更快 ​

1. 分析 ​

2. 题目 ​

3. 解题思路 ​

4. 代码 ​

6. 单元测试 ​

7. 性能测试 ​

8. 划重点 ​

八、实现二分查找 ​

1. 题目 ​

2. 解题思路 ​

3. 代码 ​

4. 单元测试 ​

5. 性能测试 ​

6. 划重点 ​

九、找出数组中和为 n 的两个元素 ​

1. 题目 ​

2. 常规思路 ​

3. 解题思路 ​

4. 代码 ​

5. 单元测试 ​

6. 性能测试 ​

7. 划重点 ​

数据结构和算法（上）

一、本节介绍

1. 数据结构和算法

2. 考察的重点

3. 注意事项

二、科普 - 算法复杂度

1. 什么是复杂度

2. 时间复杂度

3. 空间复杂度

4. 必须掌握算法复杂度

三、把一个数组旋转 k 步

1. 题目

2. 解题思路

3. 代码

4. 单元测试

5. 性能测试

6. 划重点

四、判断字符串是否括号匹配

1. 题目

2. 前置知识

3. 解题思路

4. 代码

5. 单元测试

6. 性能测试

7. 划重点

五、两个栈实现一个队列

1. 题目

2. 前置知识

3. 解题思路

4. 代码

5. 单元测试

6. 性能分析

7. 划重点

六、定义一个 JS 函数，反转单向链表

1. 前置知识

3. 解题思路

4. 代码

5. 单元测试

6. 划重点

七、（连环问）链表和数组，那个实现队列更快

1. 分析

2. 题目

3. 解题思路

4. 代码

6. 单元测试

7. 性能测试

8. 划重点

八、实现二分查找

1. 题目

2. 解题思路

3. 代码

4. 单元测试

5. 性能测试

6. 划重点

九、找出数组中和为 n 的两个元素

1. 题目

2. 常规思路

3. 解题思路

4. 代码

5. 单元测试

6. 性能测试

7. 划重点