数据结构和算法（下）

一、求一个二叉搜索树的第 k 小值

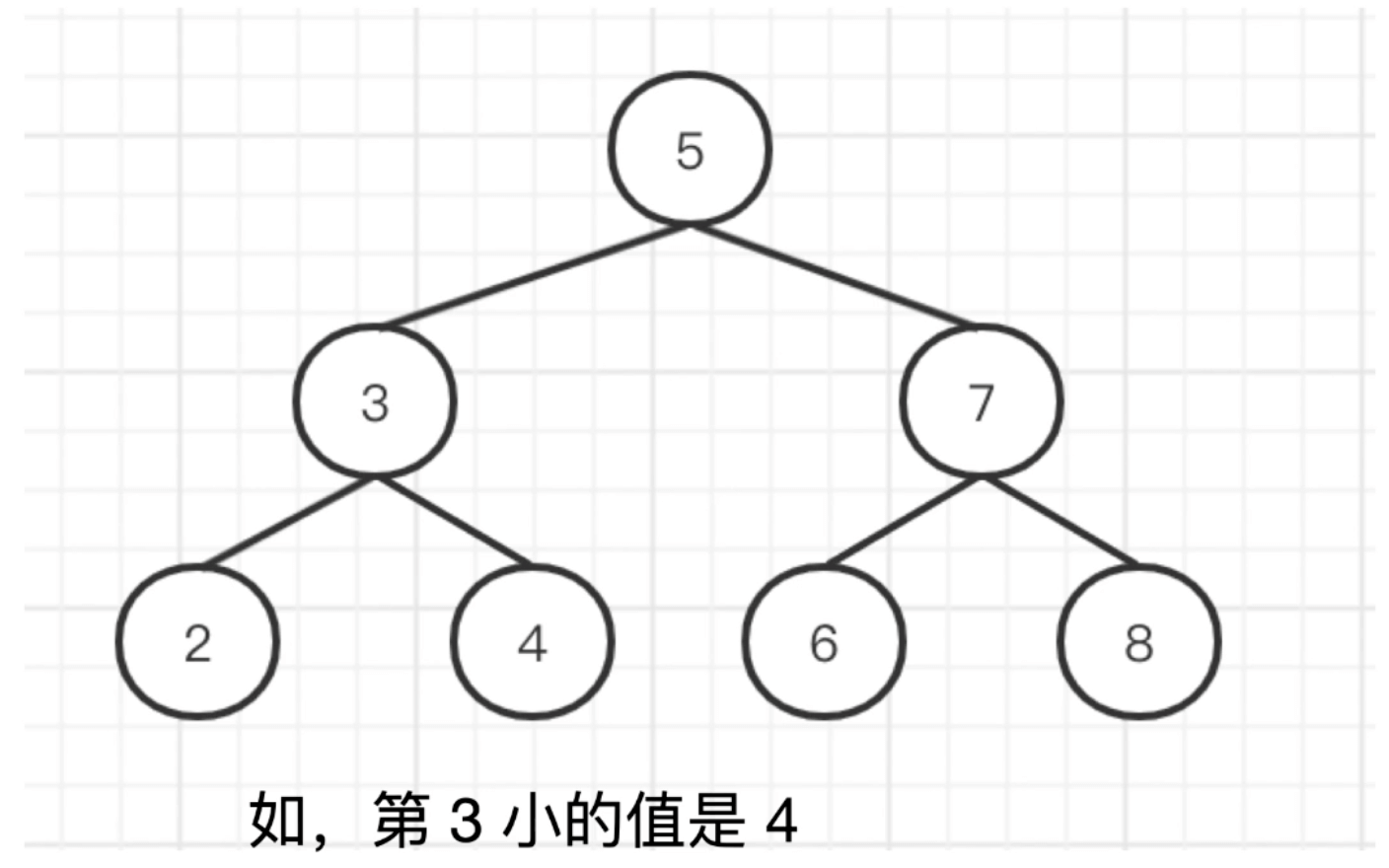
1. 前置知识

二叉树（ Binary Tree ）
1. 是一颗树
2. 每个节点最多有两个子节点
3. 树节点的数据格式 { value, left?, right? }
二叉树的遍历
1. 前序遍历：root -> left -> right
2. 中序遍历：left -> root -> right
3. 后序遍历：left -> right -> root
二叉搜索树 BST ( Binary Search Tree )
1. left ( 包括其后代 ) value <= root value
2. right ( 包括其后代 ) value >= root value
3. 可使用 二分法 进行快速查找

2. 代码演示

typescript

interface TreeNode {
    value: number,
    left: TreeNode | null,
    right: TreeNode | null
}

const bst: TreeNode = {
    value: 5,
    left: {
        value: 3,
        left: {
            value: 2,
            left: null,
            right: null
        },
        right: {
            value: 4,
            left: null,
            right: null
        }
    },
    right: {
        value: 7,
        left: {
            value: 6,
            left: null,
            right: null
        },
        right: {
            value: 8,
            left: null,
            right: null
        }
    }
}

/**
 * 二叉树前序遍历
 * @param node node
 */
// 5 3 2 4 7 6 8
function preOrderTraverse(node: TreeNode | null) {
    if (node == null) return
    console.log(node.value)
    preOrderTraverse(node.left)
    preOrderTraverse(node.right)
}

/**
 * 二叉树中序遍历
 * @param node node
 */
// 2 3 4 5 6 7 8
function inOrderTraverse(node: TreeNode | null) {
    if (node == null) return
    inOrderTraverse(node.left)
    console.log(node.value)
    inOrderTraverse(node.right)
}

/**
 * 二叉树后序遍历
 * @param node node
 */
// 2 4 3 6 8 7 5
function postOrderTraverse(node: TreeNode | null) {
    if (node == null) return
    postOrderTraverse(node.left)
    postOrderTraverse(node.right)
  	console.log(node.value)
}

3. 解题思路

BST 中序遍历，即从小到大的排序
找到排序后的第 k 值即可

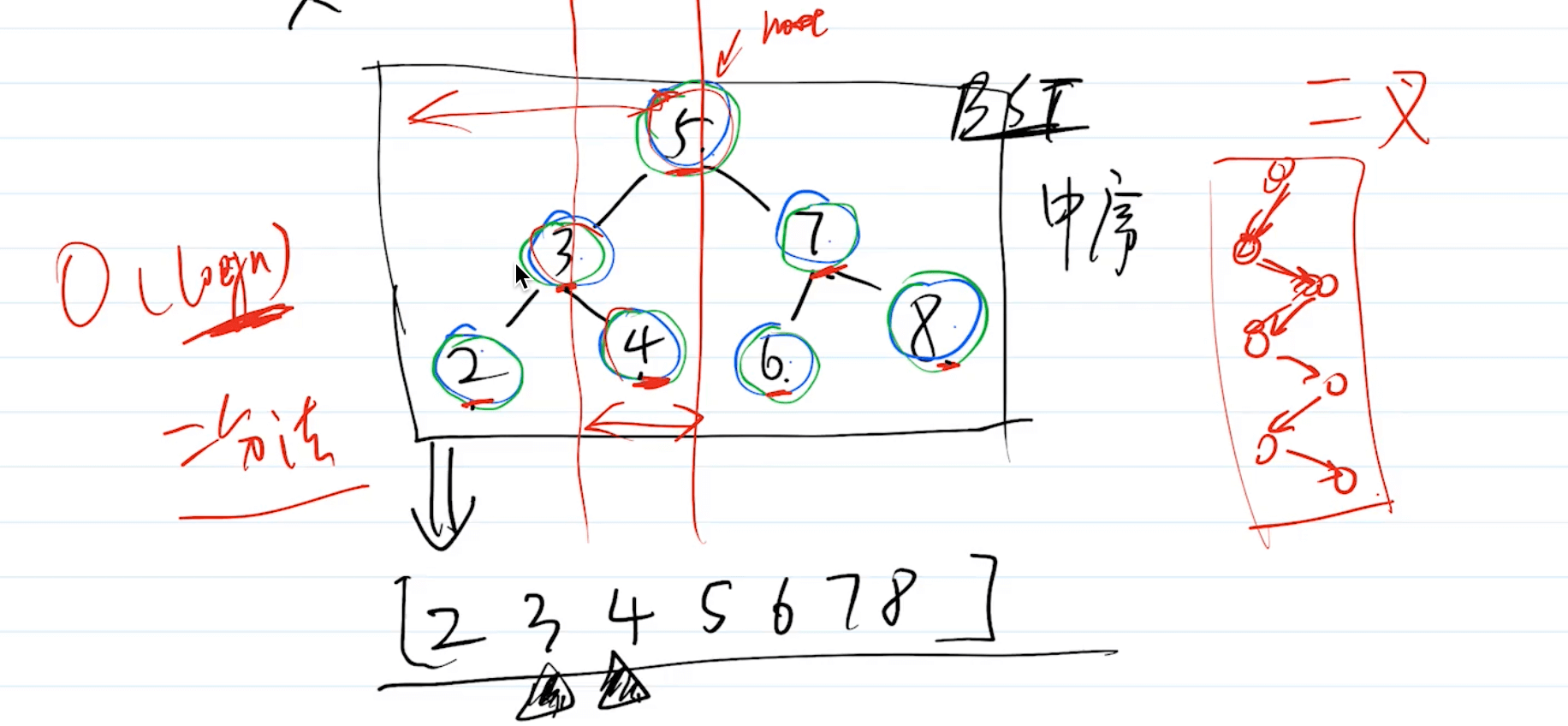
4. 代码

typescript

const array: number[] = []

/**
 * 二叉树中序遍历
 * @param node node
 */
function inOrderTraverse(node: TreeNode | null) {
    if (node == null) return
    inOrderTraverse(node.left)
    array.push(node.value)
    inOrderTraverse(node.right)
}

/**
 * 寻找 BST 里的第 k 小值
 * @param node node
 * @param k k
 */
function getKthValue(node: TreeNode, k: number): number | null {
    inOrderTraverse(node)
    return array[k - 1] || null
}

5. 单元测试

typescript

/**
 * @description 二叉搜索树第 k 小值
 * @author lzz
 */

import {bst, getKthValue} from "./8.求一个二叉搜索树的第 k 小值";

describe('二叉搜索树第 k 小值', () => {
    it('正常情况', () => {
        expect(getKthValue(bst, 3)).toBe(4)
    });

    it('k 不在正常范围之内', () => {
        expect(getKthValue(bst, 0)).toBeNull()
      	expect(getKthValue(bst, 100)).toBeNull()
    });
})

6. 划重点

二叉树，和三种（前序、中序、后序）遍历
二叉搜索树的特点：left <= root; right >= root
二叉搜索树的价值：可使用 二分法 进行快速查找

二、为何二叉树如此重要，而不是其他叉树

1. 性能、性能还是性能

数组：查询快 O(1)，增删慢 O(n)
链表：查询慢 O(n)，增删快 O(1)
二叉搜索树 BST：查询快，增删快 -- “ 木桶效应 ”

2. 平衡二叉树

BST 如果不平衡，那就又成了链表了
所有要尽量平衡：平衡二叉搜索树 BBST
BBST 增删查，时间复杂度都是 O(logn)，即树的高度

3. 红黑树

一种自平衡二叉树
分为红/黑两种颜色，通过颜色转换来维持树的平衡
相对于普通平衡二叉树，它维持平衡的效率更高

4. B 树

物理上是多叉树，但逻辑上是二叉树
一般用于高效 I/O，关系型数据库常用于 B树来组织数据

5. 小结

数组、链表，各有各的缺点
特定的二叉树（ BBST ）可以让整体效果最优
各种高级二叉树，继续优化，满足不同场景

三、堆有什么特点，和二叉树有什么关系

1. 堆栈模型

JS 代码执行时
值类型变量，存储在栈
引用类型变量，存储在堆

2. 堆

完全二叉树
最大堆：父节点 >= 子节点
最小堆：父节点 <= 子节点

3. 逻辑结构 vs 物理结构

堆，逻辑结构 是一棵二叉树
但它 物理结构 是一个数组
数组：适合连续存储 + 节省空间（回顾堆栈模型）

4. 堆 vs BST

查询比 BST 慢
增删比 BST 快，维持平衡更快
但整体的时间复杂度都在 O(logn) 级别，即树的高度

5. 堆的使用场景

特别适合 “ 堆栈模型 ”
堆的数据，都是在栈中引用的，不需要从 root 遍历
堆恰巧是数组形式，根据栈的地址，可用 O(1) 找到目标

6. 小结

堆栈模型，堆的场景
堆的特点，堆和 BST
堆的逻辑结构和物理结构

四、求斐波那契数列第 n 个值

1. 题目

用 JS 计算斐波那契数列的第 n 个值
注意时间复杂度

2. 解题思路

f(0) = 0
f(1) = 1
f(n) = f(n - 1) + f(n - 2)

3. 代码（递归，不可用）

typescript

/**
 * @description 求斐波那契数列第 n 个值
 * @author lzz
 */

/**
 * 斐波那契数列第 n 个值（递归）
 * @param n
 */
function fibonacci(n: number): number {
    if (n <= 0) return 0
    if (n === 1) return 1
    return fibonacci(n - 1) + fibonacci(n - 2)
}

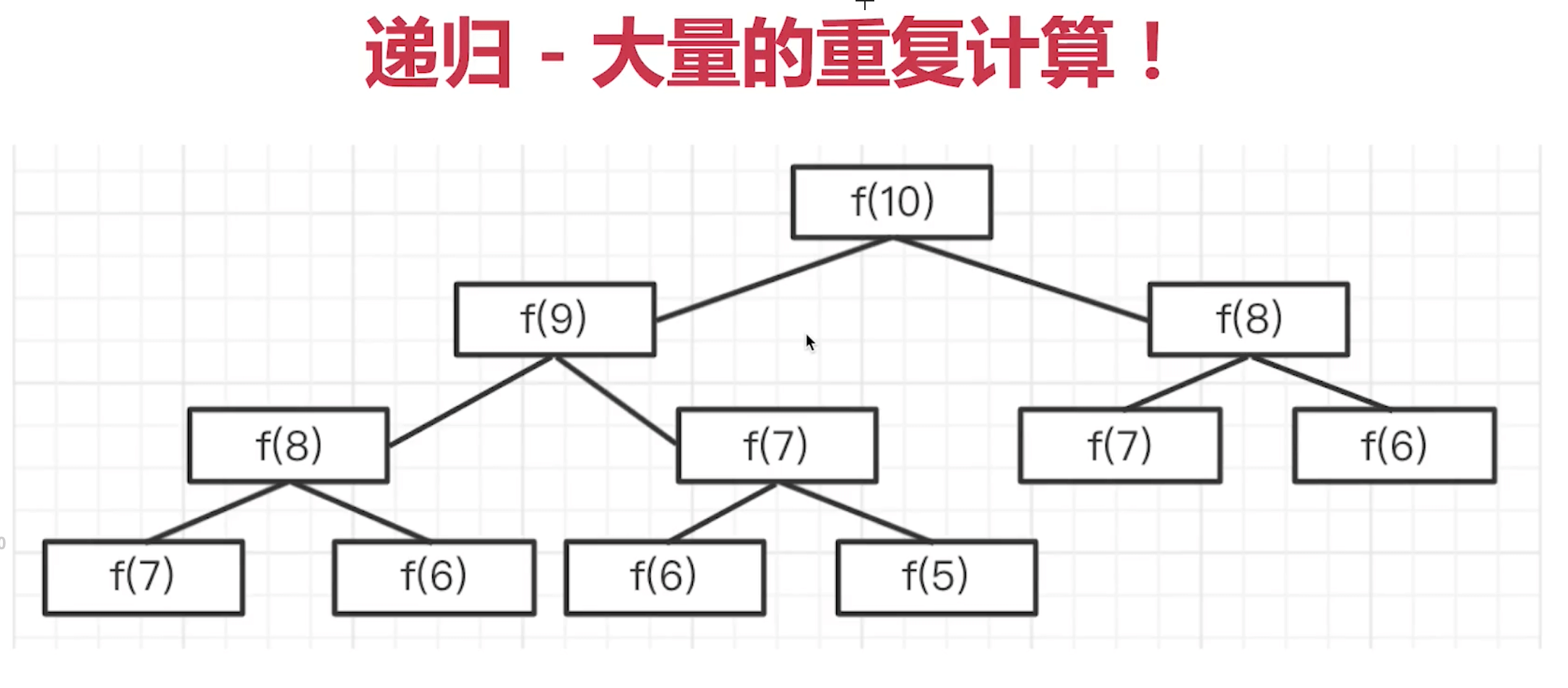
4. 分析

递归 - 大量的重复计算！
时间复杂度是 O(2^n)

5. 优化

不用递归，用循环
记录中间结果
时间复杂度为 O(n)

6. 代码（循环）

typescript

/**
 * 斐波那契数列第 n 个值 (循环)
 * @param n
 */
function fibonacci(n: number): number {
    if (n <= 0) return 0
    if (n === 1) return 1
    let n1 = 1  // 记录 n - 1 的结果
    let n2 = 0  // 记录 n - 2 的结果
    let res = 0
    // 要从 2 开始循环
    for (let i = 2; i <= n; i++) {
        res = n1 + n2
        // 记录中间结果
        n2 = n1
        n1 = res
    }
    return res
}

7. 单元测试

typescript

/**
 * @description 求斐波那契数列的第n值
 * @author lzz
 */

import {fibonacci} from './9.求斐波那契数列的第n值'

describe('求斐波那契数列的第n值', () => {
    it('0 和 1', function () {
        expect(fibonacci(0)).toBe(0)
        expect(fibonacci(1)).toBe(1)
    });
    it('除 0 和 1 外, 正常情况', function () {
        expect(fibonacci(9)).toBe(34)
    });
    it('n 小于 0', function () {
        expect(fibonacci(-1)).toBe(0)
    });
})

8. 动态规划

把一个大问题，拆解成多个小问题，逐级向下拆解
用递归的思路去分析问题，再改为循环来实现
算法三大思维：贪心、二分、动态规划

五、（连环问）青蛙跳台阶有几种方式

1. 题目

一只青蛙，一次可以跳 1 级，也可以跳 2 级
问：青蛙跳到 n 级台阶，总共有多少种方式？

2. 用动态规划分析问题

要跳到 1 级台阶，就 1 种方式 f(1) = 1
要跳到 2 级台阶，就 2 种方式 f(2) = 2
要跳到 n 级台阶，f(n) = f(n - 1) + f(n - 2)

iShot2022-03-04 17.40.47

和斐波那契数列完全一样

六、移动 0 到数组的末尾

1. 题目

如输入 [1, 0, 3, 0, 11, 0] ，输出 [1, 3, 11, 0, 0, 0]
只移动 0 ，其他顺序不变
必须在原数组进行操作

2. 如果不限制 “ 必须在原数组操作 ”

定义 part1 part2 两个数组
遍历数组，非 0 push 到 part1 ，0 push 到 part2
返回 part1.concat(part2)

3. 传统思路

遍历数组，遇到 0 则 push 到数组结尾
用 splice 截取掉当前元素
时间复杂度是 O(n^2) -- 算法不可用

4. 代码（传统思路）

typescript

/**
 * @description 移动 0 到数组末尾
 * @author lzz
 */
const array = [1, 0, 1, 1, 0, 0, 1]
/**
 * 移动 0 到数组末尾 (传统思路: 嵌套循环)
 * @param arr number arr
 */
function moveZero1(arr: number[]): void {
    const len = arr.length
    if (!len) return
    let zeroLen = 0
  // O(n^2)
    for (let i = 0; i < len - zeroLen; i++) {
        if (arr[i] === 0) {
            arr.push(0)
            arr.splice(i, 1)  // 本身就有 O(n)
            i--  // 数组截取了一个元素, i 要递减, 否则遇到连续 0 会有错误
            zeroLen++  // 累计 0 的长度
        }
    }
    return
}

5. 双指针代码思路

定义 j 指向第一个 0 ，i 指向 j 后面的第一个非 0
交换 i 和 j 的值，继续向后移动
只遍历一次，所以时间复杂度是 O(n)

6. 代码（双指针）

typescript

/**
 * 移动 0 到数组末尾 (双指针)
 * @param arr
 */
function moveZero2(arr: number[]): void {
    const len = arr.length
    if (!len) return
    let i
    let j = -1  // 指向第一个 0
    for (i = 0; i < len; i++) {
        if (arr[i] === 0) {
            // 第一个 0
            if (j < 0) {
                j = i
            }
        }
        if (arr[i] !== 0 && j !== -1) {
            // 交换
            const temp = arr[i]
            arr[i] = arr[j]
            arr[j] = temp
            j++
        }
    }
}

7. 单元测试

typescript

/**
 * @description 移动 0 到数组末尾
 * @author lzz
 */
import {moveZero1, moveZero2} from "./10.移动 0 到数组末尾";

describe('移动 0 到数组末尾', () => {
    it('正常类型', function () {
        const array = [1, 0, 3, 4, 0, 11, 0]
        moveZero2(array)
        expect(array).toEqual([1, 3, 4, 11, 0, 0, 0])
    });
    it('连续 0 情况', function () {
        const array = [1, 0, 3, 4, 0, 0, 0, 11, 0]
        moveZero2(array)
        expect(array).toEqual([1, 3, 4, 11, 0, 0, 0, 0, 0])
    });
    it('没有 0', function () {
        const array = [1, 3, 4, 11]
        moveZero2(array)
        expect(array).toEqual([1, 3, 4, 11])
    });
    it('全是 0', function () {
        const array = [0, 0, 0, 0]
        moveZero2(array)
        expect(array).toEqual([0, 0, 0, 0])
    });
})

8. 性能测试

typescript

const testArr = []
for (let i = 0; i < 20 * 10000; i++) {
    i % 10 ? testArr.push(i) : testArr.push(0)
}

console.time('嵌套循环')
moveZero1(testArr)
console.timeEnd('嵌套循环')  // 5.477s

console.time('双指针')
moveZero2(testArr)
console.timeEnd('双指针')  // 3.22ms

9. 划重点

向面试官确认：是否必须修改原数组？
数组是连续存储，要慎用 unshift 、splice 等 API
双指针思路

七、字符串中连续最多的字符，以及次数

1. 题目

如，输入 ‘ abbcccddeeee1234 ’ ，计算得到：
连续最多的字符是 ‘ e ’ ，4 次

2. 传统思路

嵌套循环，找出每个字符的连接次数，并记录
看似时间复杂度是 O(n^2)
但是实际时间复杂度是 O(n) ，因为有 “ 跳步 ”

3. 代码 ( 嵌套循环 )

typescript

/**
 * 获取字符串中连续最多的字符及次数(嵌套循环)
 * @param str
 */
function findContinuousChar1(str: string): IRes {
    const res: IRes = {
        str: '',
        times: 0
    }
    const len = str.length
    if (!len) return res
    let tempLength = 0  // 临时记录当前连续字符的长度
    // O(n)
    for (let i = 0; i < len; i++) {
        tempLength = 0
        for (let j = i; j < len; j++) {
            if (str[i] === str[j]) {
                tempLength++
            }
            if (str[i] !== str[j] || j === len - 1) {
                // 不相等, 或者已经到了最后一个元素, 要判断最大值
                if (tempLength > res.times) {
                    res.str = str[i]
                    res.times = tempLength
                }
                if (i < len - 1) {
                    i = j - 1  // 跳步
                }
                break
            }
        }
    }
    return res
}

4. 双指针思路

定义指针 i 和 j ，j 不动，i 继续移动
如果 i 和 j 的值一直相等，则 i 继续移动
直到 i 和 j 的值不相等，记录处理，让 j 追上 i 。重复第一步

5. 代码（双指针）

typescript

/**
 * 获取字符串中连续最多的字符及次数(双指针)
 * @param str
 */
function findContinuousChar2(str: string): IRes {
    const res: IRes = {
        str: '',
        times: 0,
    }
    const len = str.length
    if (!len) return res
    let tempLength = 0  // 临时记录当前连续字符的长度
    let i
    let j = 0
    // O(n)
    for (i = 0; i < len; i++) {
        if (str[i] === str[j]) {
            tempLength++
        }
        if (str[i] !== str[j] || i === len - 1) {
            // 不相等, 或者已经到了最后一个元素, 要判断最大值
            if (tempLength > res.times) {
                res.str = str[j]
                res.times = tempLength
            }
            tempLength = 0  // 重置

            if (i < len - 1) {
                j = i  // 让 j 追上 i
                i--  // 细节
            }
        }
    }
    return res
}

6. 单元测试

typescript

/**
 * @description 获取字符串中连续最多的字符及次数
 * @author lzz
 */

import {findContinuousChar1, findContinuousChar2} from './11.获取字符串中连续最多的字符及次数'

describe('获取字符串中连续最多的字符及次数', () => {
    it('正常情况', function () {
        expect(findContinuousChar2('aabbcccddeeee11223')).toEqual({
            str: 'e',
            times: 4
        })
    });
    it('空字符串', function () {
        expect(findContinuousChar2('')).toEqual({
            str: '',
            times: 0
        })
    });
    it('无连续', function () {
        expect(findContinuousChar2('abcdefghijk')).toEqual({
            str: 'a',
            times: 1
        })
    });
    it('全部连续', function () {
        expect(findContinuousChar2('aaaaaaaaaaa')).toEqual({
            str: 'a',
            times: 11
        })
    });
})

7. 性能测试

typescript

let str = ''
for (let i = 0; i < 100 * 10000; i++) {
    str += i.toString()
}
console.time('findContinuousChar1')
findContinuousChar1(str)
console.timeEnd('findContinuousChar1');  // 159.09ms

console.time('findContinuousChar2')
findContinuousChar2(str)
console.timeEnd('findContinuousChar2');  // 150.831ms

8. 其他方式

正则表达式 -- 效率非常低，慎用！！！
累计各个元素的连续长度，最后求最大值 -- 徒增空间复杂度
PS：算法题尽量用 “ 低级 ” 代码，慎用语法糖或者高级 API

9. 划重点

要注意实际复杂度，不要被代码表面迷惑（类似于跳步）
双指针常用于解决嵌套循环
算法题慎用正则表达式（实际工作可以用）

八、用 JS 实现快速排序

1. 固定算法，固定思路

找到中间位置 midValue
遍历数组，小于 midvalue 放在 left ，否则放在 right
继续递归，最后 concat 拼接返回

2. 细节

获取 midValue 的两种方式：
使用 splice ，会修改原数组
使用 slice ，不会修改原数组 -- 更加推荐

3. 代码

typescript

/**
 * @description JS 实现快速排序
 * @author lzz
 */

/**
 * 快速排序 - splice 方法
 * @param arr
 */
function quickSort1(arr: number[]): number[] {
    const len = arr.length
    if (!len) return arr
    const midIndex = Math.floor(len / 2)
    const midValue = arr.splice(midIndex, 1)[0]
    const left: number[] = []
    const right: number[] = []
    // 注意: 这里不能使用 len , 应使用 arr.length , 因为 splice 已经改变数组 arr
    // O(nlogn)
    for (let i = 0; i < arr.length; i++) {
        const n = arr[i]
        if (n < midValue) {
            // 小于 midValue 则放在左侧
            left.push(n)
        } else {
            // 大于 midValue 则放在右侧
            right.push(n)
        }
    }
    return quickSort1(left).concat(
        [midValue],
        quickSort1(right)
    )
}

/**
 * 快速排序 - slice 或 取索引 方法
 * @param arr
 */
function quickSort2(arr: number[]): number[] {
    const len = arr.length
    if (!len) return arr
    const midIndex = Math.floor(len / 2)
    // 为了对比 splice , 可使用 arr[midIndex]
    const midValue = arr.slice(midIndex, midIndex + 1)[0]
    // const midValue = arr[midIndex]
    const left: number[] = []
    const right: number[] = []
    // O(nlogn)
    for (let i = 0; i < len; i++) {
        // 要忽略中间值
        if (i !== midIndex) {
            const n = arr[i]
            if (n < midValue) {
                // 小于 midValue 则放在左侧
                left.push(n)
            } else {
                // 大于 midValue 则放在右侧
                right.push(n)
            }
        }
    }
    return quickSort2(left).concat(
        [midValue],
        quickSort2(right)
    )
}

4. 单元测试

typescript

/**
 * @description 快速排序
 * @author lzz
 */

import {quickSort1, quickSort2} from './12. 快速排序'

describe('快速排序', () => {
    it('正常情况 ', function () {
        const arr = [1, 23, 2, 4, 4, 66, 7, 8]
        expect(quickSort2(arr)).toEqual([1, 2, 4, 4, 7, 8, 23, 66])
    });
    it('有负数 ', function () {
        const arr = [1, 23, -2, 4, 4, 66, 7, 8]
        expect(quickSort2(arr)).toEqual([-2, 1, 4, 4, 7, 8, 23, 66])
    });
    it('同一元素 ', function () {
        const arr = [1, 1, 1, 1, 1]
        expect(quickSort2(arr)).toEqual([1, 1, 1, 1, 1])
    });
    it('空数组 ', function () {
        expect(quickSort2([])).toEqual([])
    });
})

5. 时间复杂度

有遍历，有二分 -- O(nlogn)
常规排序，嵌套循环，复杂度是 O(n^2)

6. 性能测试

typescript

// 性能测试
const array = []
for (let i = 0; i < 10 * 10000; i++) {
    array.push(Math.floor(Math.random() * 1000))
}
console.time('splice')
quickSort1(array)
console.timeEnd('splice')  // 73.464ms

console.time('slice')
quickSort2(array)
console.timeEnd('slice')  // 71.336ms

7. splice 和 slice 没有区分出来

算法本身的时间复杂度就够高 O(nlogn)
外加，splice 是逐步二分之后执行的，二分会快速消减数量级
如果单独比较 splice 和 slice ，效果会非常明显

8. 划重点

常见排序算法 -- 固定思维
有二分，时间复杂度就包含 O(logn)
注意数组操作：splice 和 slice

九、对称数

1. 题目

求 1-10000 之间所有的对称数（回文）
例如：1, 2, 11, 22, 101, 232, 1221...

2. 解题思路

思路一：使用数组反转、比较
1. 数字转换为字符串，在转换为数组
2. 数组 reverse ，再 join 为字符串
3. 前后字符串进行对比
思路二：字符串头尾比较
1. 数字转换为字符串
2. 字符串头尾字符比较
3. ( 也可以用栈，像括号匹配，但要注意奇偶数 )
思路三：生成翻转数
1. 使用 % 和 Math.floor 生成反转数
2. 前后数字进行对比
3. ( 全程操作数字，没有字符串类型 )

3. 代码

typescript

/**
 * 求 1-max 之间所有的对称数 - 反转比对
 * @param max 最大值
 */
function palindromeNum1(max: number): number[] {
    const res: number[] = []
    if (max <= 0) return res
    for (let i = 1; i <= max; i++) {
        const str = i.toString()
        // 转换为字符串，转换为数组，再反转，比较
        if (str === str.split('').reverse().join('')) {
            res.push(Number(str))
        }
    }
    return res
}

/**
 * 求 1-max 之间所有的对称数 - 字符串前后比对
 * @param max 最大值
 */
function palindromeNum2(max: number): number[] {
    const res: number[] = []
    if (max <= 0) return res
    for (let i = 1; i <= max; i++) {
        const str = i.toString()
        const len = str.length
        let index = 0
        for (let j = 0; j < len; j++) {
            if (str[j] === str[len - 1 - j]) {
                index++
            }
        }
        if (index === len) res.push(i)
    }
    return res
}

/**
 * 求 1-max 之间所有的对称数 - 生成反转数
 * @param max 最大值
 */
function palindromeNum3(max: number): number[] {
    const res: number[] = []
    if (max <= 0) return res
    for (let i = 1; i <= max; i++) {
        let n = i
        let rev = 0  // 储存反转数
        // 生成反转数
        while (n > 0) {
            rev = rev * 10 + n % 10
            n = Math.floor(n / 10)
        }
        if (i === rev) res.push(i)
    }
    return res
}

4. 单元测试

typescript

/**
 * @description 求 1-10000 之间所有的对称数（回文）
 * @author lzz
 */
import {palindromeNum1, palindromeNum2, palindromeNum3} from './13.对称数'

describe('对称数', () => {
    it('正常情况 ', function () {
        expect(palindromeNum1(100).length).toBe(18)
    });
    it('max 小于等于 0 ', function () {
        expect(palindromeNum1(0)).toEqual([])
    });
})

5. 性能测试

typescript

// 性能测试
console.time('palindromeNum1')
palindromeNum1(100 * 10000)
console.timeEnd('palindromeNum1')  // 346ms

console.time('palindromeNum2')
palindromeNum2(100 * 10000)
console.timeEnd('palindromeNum2')  // 106ms

console.time('palindromeNum3')
palindromeNum3(100 * 10000)
console.timeEnd('palindromeNum3')  // 39ms

6. 性能分析

思路1 - 看似是 O(n) ，但数组转换、操作都需要时间，所以慢
思路2 vs 思路3 ，操作数字更快（电脑原型就是计算器）
思路2 要用栈，不合适。因为栈也一般用数组实现，会慢

7. 划重点

尽量不要转换数据结构，尤其数组这种有序结构
尽量不要用内置 API ，如 reverse ，不好识别复杂度
数字操作最快，其次是字符串

十、高效的字符串前缀匹配

1. 题目

有一个英文单词库（数组），里面有十几万个英文单词
输入一个字符串，快速判断是不是某一个单词的前缀
说明思路，不用写代码

2. 解题思路

常规思路
1. 遍历单词库数组
2. indexOf 判断前缀
3. 实际时间复杂度超过了 O(n) ，因为要考虑 indexOf 的计算量
优化
1. 英文字母一共 26 个，可以提前把单词库数拆分成 26 个
2. 既然第一层拆分 26 个，第二层、第三层，还可以继续拆分
3. 最后把单词库拆分成一棵树

3. 性能分析

如遍历数组，时间复杂度至少 O(n) 起步（ n 是数组长度）
而改成数，时间复杂度降低到 O(m) （ m 是单词长度）
PS：哈希表（对象）通过 key 查询，时间复杂度是 O(1)

4. 划重点

考虑优化原始数据结构（需先沟通）
有明确范围的数据（如 26 个英文字母），考虑使用哈希表（对象）
以空间换时间，定义数据结构最重要

十一、数字千分位格式化

1. 题目

将数字千分位格式化，输出字符串
如输入数字 12050100 ，输出字符串 12,050,100
( 注意：逆序判断 )

2. 常见思路

转换为数组，reverse ，每 3 位拆分
使用正则表达式
使用字符串拆分

3. 代码

typescript

/**
 * @description 数字千分位格式化
 * @author lzz
 */

/**
 * 千分位格式化（使用数组）
 * @param n
 */
export function format1(n: number): string {
    n = Math.floor(n)  // 只考虑整数部分
    const s = n.toString()
    const arr = s.split('').reverse()
    return arr.reduce((prev, val, index) => {
        if (index % 3 === 0) {
            if (prev) {
                return val + ',' + prev
            } else {
                return val
            }
        } else {
            return val + prev
        }
    }, '')
}

/**
 * 千分位格式化（使用字符串）
 * @param n
 */
export function format2(n: number): string {
    const num = Math.floor(n)
    const str = num.toString()
    const len = str.length
    let res = ''
    for (let i = len - 1; i >= 0; i--) {
        const j = len - i
        if (j % 3 === 0 && i !== 0) {
            res = ',' + str[i] + res
        } else {
            res = str[i] + res
        }
    }
    return res
}

4. 单元测试

typescript

/**
 * @description 数字千分位格式化
 * @author lzz
 */

import {format1, format2} from './14.数字千分位格式化'

describe('数字千分位格式化', () => {
    it('正常情况', function () {
        expect(format2(100200300)).toBe('100,200,300')
    });
    it('千位以下', function () {
        expect(format2(0)).toBe('0')
        expect(format2(100)).toBe('100')
    });
})

5. 性能分析

使用数组，转换影响性能
使用正则表达式，性能较差
使用字符串，性能较好 -- 推荐答案

6. 划重点

顺序：从尾到头
尽量不要转化数据结构
慎用正则表达式

十二、切换字母大小写

1. 题目

输入一个字符串，切换其中字母的大小写
如，输入字符串 12aBc34 ，输出字符串 12AbC34

2. 常见思路

正则表达式
通过 ASCII 码判断

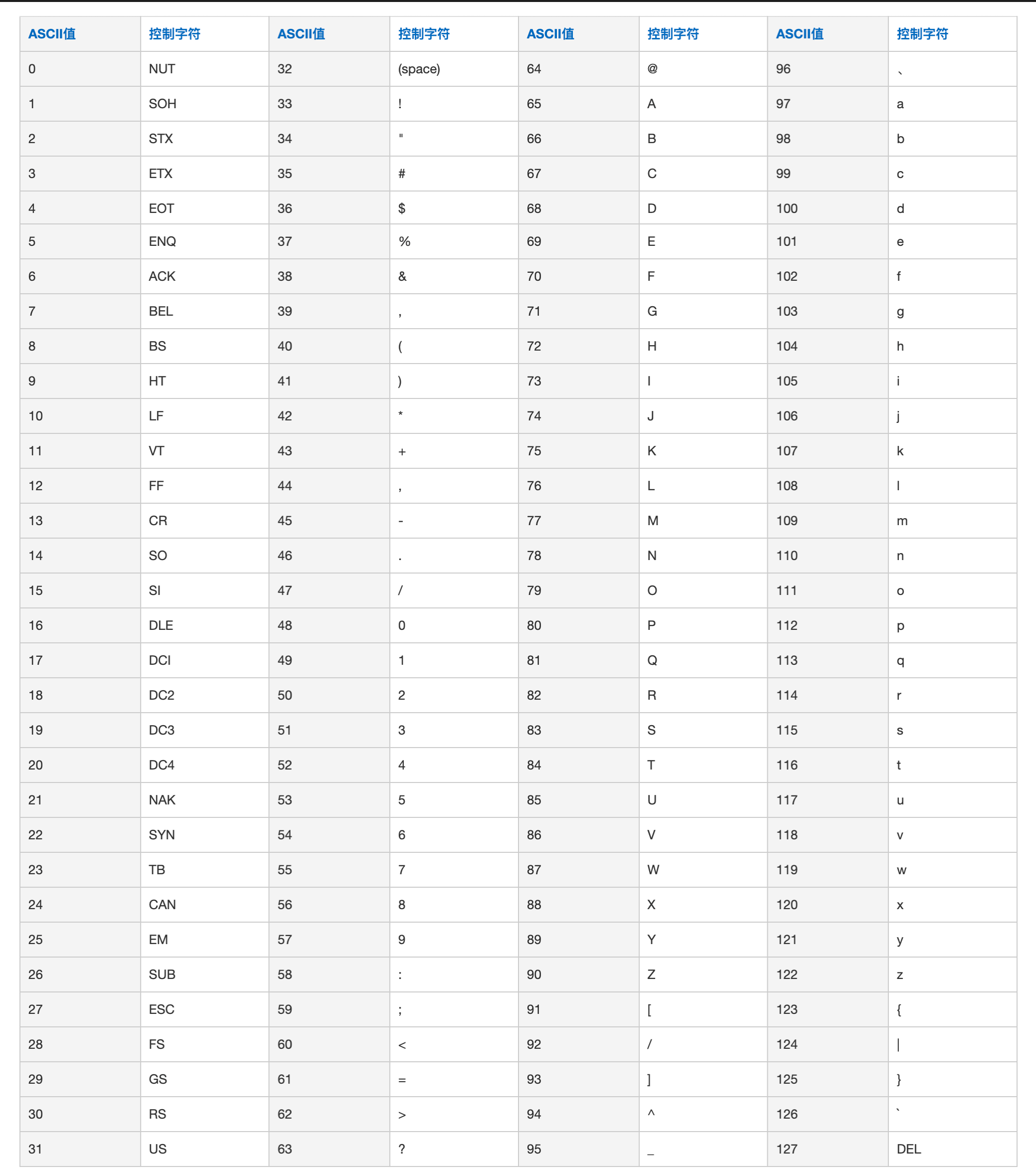
3. 代码

typescript

/**
 * @description 切换字母大小写
 * @author lzz
 */

/**
 * 切换字母大小写 - 正则
 * @param str
 */
function changeCase1(str: string): string {
    let res = ''
    const reg1= /[a-z]/
    const reg2= /[A-Z]/
    for (let i = 0; i < str.length; i++) {
        if (reg1.test(str[i])) {
            // 小写字母
            res += str[i].toUpperCase()
        } else if (reg2.test(str[i])) {
            // 大写字母
            res += str[i].toLowerCase()
        } else {
            res += str[i]
        }
    }
    return res
}

/**
 * 切换字母大小写 - ASCII
 * @param str
 */
function changeCase2(str: string): string {
    let res = ''
    for (let i = 0; i < str.length; i++) {
        const code = str[i].charCodeAt(0)
        if (code >= 65 && code <= 90) {
            // 大写字母
            res += String.fromCharCode(code + 32)
            // 也可使用 API 但是经过测试 会比上面方法慢
            // res += str[i].toLowerCase()
        } else if (code >= 97 && code <= 122) {
            // 小写字母
            res += String.fromCharCode(code - 32)
            // res += str[i].toUpperCase()
        } else {
            res += str[i]
        }
    }
    return res
}

4. 单元测试

typescript

/**
 * @description 切换字母大小写
 * @author lzz
 */
import {changeCase1, changeCase2} from './15.切换字母大小写'

describe('切换字母大小写', () => {
    it('正常情况', function () {
        expect(changeCase2('2aBcD1')).toBe('2AbCd1')
    });
    it('空字符', function () {
        expect(changeCase2('')).toBe('')
    });
    it('非字母', function () {
        expect(changeCase2('2你!#')).toBe('2你!#')
    });
})

5. 性能测试

typescript

const s = '123asd321BhS33BSC'
console.time('reg')
for (let i = 0; i < 100 * 10000; i++) {
    changeCase1(s)
}
console.timeEnd('reg')  // 875ms

console.time('ascii')
for (let i = 0; i < 100 * 10000; i++) {
    changeCase2(s)
}
console.timeEnd('ascii')  // 224ms

6. 性能分析

使用正则，性能较差
使用 ASCII 码，性能较好 -- 推荐答案

7. 划重点

慎用正则表达式
掌握常见的 ASCII 码

十三、为什么 0.1 + 0.2 !== 0.3

1. 计算机使用二进制存储数据

整数转换二进制没有误差，如 9 转换为二进制是 1001
而小数可能无法用二进制准确的表达，如 0.2 转换为 1.1001100...
不光 JavaScript 其他编程语言也如此

总结

1. 内容总结

前端数据结构和算法的常见题目
包含了数组、栈、队列、链表、二叉树这些常见的数据结构
常用的算法思维如贪婪、二分、动态规划，以及如何计算时间复杂度

2. 划重点

有序数据考虑用二分
双指针可以解决嵌套循环

3. 注意事项

注意区分逻辑结构和物理结构，否则思维会很混乱
要有 “算法敏感度”，条件反射般的根据数据结构分析时间复杂度

数据结构和算法（下） ​

一、求一个二叉搜索树的第 k 小值 ​

1. 前置知识 ​

2. 代码演示 ​

3. 解题思路 ​

4. 代码 ​

5. 单元测试 ​

6. 划重点 ​

二、为何二叉树如此重要，而不是其他叉树 ​

1. 性能、性能还是性能 ​

2. 平衡二叉树 ​

3. 红黑树 ​

4. B 树 ​

5. 小结 ​

三、堆有什么特点，和二叉树有什么关系 ​

1. 堆栈模型 ​

2. 堆 ​

3. 逻辑结构 vs 物理结构 ​

4. 堆 vs BST ​

5. 堆的使用场景 ​

6. 小结 ​

四、求斐波那契数列第 n 个值 ​

1. 题目 ​

2. 解题思路 ​

3. 代码（递归，不可用） ​

4. 分析 ​

5. 优化 ​

6. 代码（循环） ​

7. 单元测试 ​

8. 动态规划 ​

五、（连环问）青蛙跳台阶有几种方式 ​

1. 题目 ​

2. 用动态规划分析问题 ​

六、移动 0 到数组的末尾 ​

1. 题目 ​

2. 如果不限制 “ 必须在原数组操作 ” ​

3. 传统思路 ​

4. 代码（传统思路） ​

5. 双指针代码思路 ​

6. 代码（双指针） ​

7. 单元测试 ​

8. 性能测试 ​

9. 划重点 ​

七、字符串中连续最多的字符，以及次数 ​

1. 题目 ​

2. 传统思路 ​

3. 代码 ( 嵌套循环 ) ​

4. 双指针思路 ​

5. 代码（双指针） ​

6. 单元测试 ​

7. 性能测试 ​

8. 其他方式 ​

9. 划重点 ​

八、用 JS 实现快速排序 ​

1. 固定算法，固定思路 ​

2. 细节 ​

3. 代码 ​

4. 单元测试 ​

5. 时间复杂度 ​

6. 性能测试 ​

7. splice 和 slice 没有区分出来 ​

8. 划重点 ​

九、对称数 ​

1. 题目 ​

2. 解题思路 ​

3. 代码 ​

4. 单元测试 ​

5. 性能测试 ​

6. 性能分析 ​

7. 划重点 ​

十、高效的字符串前缀匹配 ​

1. 题目 ​

2. 解题思路 ​

3. 性能分析 ​

4. 划重点 ​

十一、数字千分位格式化 ​

1. 题目 ​

2. 常见思路 ​

3. 代码 ​

4. 单元测试 ​

数据结构和算法（下）

一、求一个二叉搜索树的第 k 小值

1. 前置知识

2. 代码演示

3. 解题思路

4. 代码

5. 单元测试

6. 划重点

二、为何二叉树如此重要，而不是其他叉树

1. 性能、性能还是性能

2. 平衡二叉树

3. 红黑树

4. B 树

5. 小结

三、堆有什么特点，和二叉树有什么关系

1. 堆栈模型

2. 堆

3. 逻辑结构 vs 物理结构

4. 堆 vs BST

5. 堆的使用场景

6. 小结

四、求斐波那契数列第 n 个值

1. 题目

2. 解题思路

3. 代码（递归，不可用）

4. 分析

5. 优化

6. 代码（循环）

7. 单元测试

8. 动态规划

五、（连环问）青蛙跳台阶有几种方式

1. 题目

2. 用动态规划分析问题

六、移动 0 到数组的末尾

1. 题目

2. 如果不限制 “ 必须在原数组操作 ”

3. 传统思路

4. 代码（传统思路）

5. 双指针代码思路

6. 代码（双指针）

7. 单元测试

8. 性能测试

9. 划重点

七、字符串中连续最多的字符，以及次数

1. 题目

2. 传统思路

3. 代码 ( 嵌套循环 )

4. 双指针思路

5. 代码（双指针）

6. 单元测试

7. 性能测试

8. 其他方式

9. 划重点

八、用 JS 实现快速排序

1. 固定算法，固定思路

2. 细节

3. 代码

4. 单元测试

5. 时间复杂度

6. 性能测试

7. splice 和 slice 没有区分出来

8. 划重点

九、对称数

1. 题目

2. 解题思路

3. 代码

4. 单元测试

5. 性能测试

6. 性能分析

7. 划重点

十、高效的字符串前缀匹配

1. 题目

2. 解题思路

3. 性能分析

4. 划重点

十一、数字千分位格式化

1. 题目

2. 常见思路

3. 代码

4. 单元测试